Question

A theater can seat 952 people the number of rows is 6 less than the number of seats in each row how many rows of seats are there

Answer 1

If we arrange the seats in r rows with s seats in each row, we have

`rs=952`

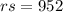
Since the number of rows is 6 less than the number of seats in each row, we have

`r=s-6`

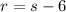
Substitute this in the first equation to get

`(s-6)s=952 \iff s^2-6s-952=0`

This equation has solutions -28 and 34. We can't accept negative solutions (we would have -28 seats in each row...what would that mean??), the only feasible solution is 34.

So, we have

`r=s-6=34-6=28`

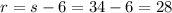
rows with 34 seats per row.