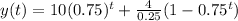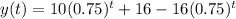Question

134. A patient in a hospital needs to maintain a certain amount of a medication in her bloodstream to fight an infection. Suppose the initial dosage is 10 mg, and the patient is given an additional maintenance dose of 4 mg every hour. Assume that the amount of medication in the bloodstream is reduced by 25% every hour.

d. Rewrite this function as the difference of two functions (one a constant function and the other an exponential function), and use that difference to justify why the amount of medication in the patient’s bloodstream will not exceed 16 mg after each dose is administered.

Answer 1

`y(t)=16-6(0.75)^t`

The function is the difference between a constant and an exponential function, the exponential function approaches to 0 as t increases. So the amount of the medication is 16 minus a quantity that is ever decreasing without take negative values. Then, that difference will ever be a number minor than 16.

Explanation:

The problem requires to write a function for the statement. The statement is about amount of medication that remains in the bloodstream each hour "t" which we going to label as "y(t)".

The statement says that there are an initial dosage of 10 mg and that the amount of medication in the bloodstream is reduced by 25% every hour. With that data we can estimate the amount of the initial dosage that remains after "t" hours. For that we need to take into account that when an original amount is reduced by a consistent rate over a period of time, as in this case, exponential decay is occurring. Exponential decay function can be written as follows:

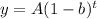`y=A(1-b)^t` with y= quantity that remains, A=initial quantity, b= percentage change (in decimal form), t is the variable time.

In this case A=10mg and b=25% (0.25 in decimal form) we can write

`y=10(0.75)^t`

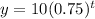
Besides, the statement says that the patient is given an additional maintenance dose of 4 mg every hour, and again that dosage also would be reduced 25% each hour. So we have that

hours amount of maintanance dosage that remains

0 0

1 4

2 4(1+0.75)

3 4(1+0.75+0.75^2)

4 4(1+0.75+0.75^2+0.75^3)

5 4(1+0.75+0.75^2+0.75^3+0.75^4)

m 4(1+0.75+0.75^2+0.75^3+0.75^4+...+0.75^(m-1))

Note that we have a sum of terms, so we can write as partial sum as follows

`4(\Sigma^m_(t=1) (0.75)^((t-1)))`

In series tables you can see that this partial sum is equals to a function

`4(\Sigma^m_(t=1) (0.75)^((t-1)))=4((1-0.75^m)/(1-0.75))`

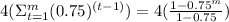
So the complete function for the medicament that remains in the blood is

`y(t)=10(0.75)^t+4((1-0.75^t)/(1-0.75))`

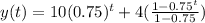
Now we should reorganize the function y as follows

`y(t)=10(0.75)^t+(4)/(0.25)(1-0.75^t)`

`y(t)=10(0.75)^t+16-16(0.75)^t`

`y(t)=16-6(0.75)^t`