Question

A parabola is defined as the set of points in the plane that are equidistant from a fixed point (called the focus of the parabola) and a fixed line (called the directrix of the parabola).Consider the parabola with focus point (1,1) and directrix the horizontal line y=−3.Plot the focus and draw the directrix graph.

Answer 1

`y=(1)/(8)(x-1)^2-1`

Explanation:

A parabola is defined as the set of points in the plane that are equidistant from a fixed point and a fixed line.

• Fixed point called focus.

• Fixed line called directirx.

Let point on parabola be (x,y)

Distance from focus(1,1) and point (x,y):

`d=√((x-1)^2+(y-1)^2)`

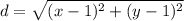
Distance from point (x,y) and line y=-3 ( x would be vary) (x,-3)

`d=√((x-x)^2+(y+3)^2)`

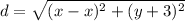
Both distance must be equal for parabola

`√((x-1)^2+(y-1)^2)=√((x-x)^2+(y+3)^2)`

`(x-1)^2+(y-1)^2=(y+3)^2`

`x^2+1-2x+y^2+1-2y=y^2+9+6y`

`x^2+2x+2=9+6y+2y`

`y=(1)/(8)(x^2+2x-7)`

`y=(1)/(8)(x-1)^2-1`

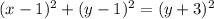
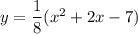
Please find attachment for graph. Focus and directrix shown in graph.