Question

Are the two parabolas defined below similar or congruent or both? Justify your reasoning. Parabola 1: The parabola with a focus of (0,2) and a directrix line of y= −4. Parabola 2: The parabola that is the graph of the equation y=(1/6)x².

Answer 1

They are similar by a factor of 14

Explanation:

From the general equation of a parabola opening up (since the directrix is on the y axis and the focus is upwards this line) the focus coordinates are:

`Focus = (h,k+p) = (0,2)`

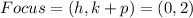
So h=0 and k+p=2, for the directrix:

`y = k-p=-4`

solving k and p from the two equations above:

`k=-1 and p=3`

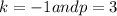
So for Parabola 1 the equation would be:

`x^(2) =4*3(y+1)`

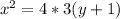
For Parabola 2 the general equation is:

`x^(2) =4*(3/2)(y)`

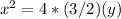
here h=0, k=0, p=3/2 so focus is (0,3/2), directix is y=-3/2, they have the same orientation.

they are not congruent. For them to be similar it must comply:

`x_(1)=k x_(2)\\y_(1)=ky_(2) => (1/12)x_(1) ^(2) -1 = k(1/6)x_(2) ^(2)`

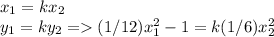
replacing
`x_(1)` and solving for k:

`(1/12)(kx_(2)) ^(2) -1 = k(1/6)x_(2) ^(2)\\ (1/12)k^(2) x_(2)^(2)-1 = k(1/6)x_(2) ^(2)\\k-12 = (12/6)=2\\k = 2+12=14\\`

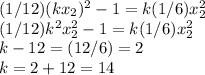
They are similar by a factor of 14