Answer:
See explanation below.
Explanation:
We need to prove that there are no solutions of the equation: x =

Let's start trying to solve this equation:
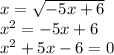
To solve this equation, by factorizing the equation we get:

- Now we're going to substitute these numbers in the original equation:
For x = -6 we have:
x =
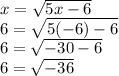
But √-36 has no solution in the real numbers and therefore it cannot equal 6.
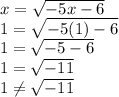
Since the left side is different than the right one, this is not a solution.
Therefore the equation has no solution in the real numbers