Question

Find the distance between the centers of the circles x²+y²-2x+4y-11=0 and x²+y²+4x+2y-9=0.

Answer 1

`√(10)`

Explanation:

The standard form of a circle is

`(x-h)^2+(y-k)^2=r^2` .... (1)

where, (h,k) is center of the circle and r is radius.

If a expression is
`x^2+bx`, then we need to add
`((b)/(2))^2` to make it perfect square.

The equation of first circle is

`x^2+y^2-2x+4y-11=0`

`(x^2-2x)+(y^2+4y)=11`

`(x^2-2x+1)-1+(y^2+4y+4)-4=11`

`(x-1)^2+(y-2)^2-5=11`

Add 5 on both sides.

`(x - 1)^2 + (y + 2)^2 = 16` .... (2)

On comparing (1) and (2) we get

`h=1,k=-2`

The center of first circle is (1,-2).

The equation of second circle is

`x^2+y^2+4x+2y-9=0`

`(x^2+4x)+(y^2+2y)=9`

`(x^2+4x+4)-4+(y^2+2y+1)-1=9`

`(x+2)^2+(y+1)^2-5=9`

Add 5 on both sides.

`(x + 2)^2 + (y + 1)^2 = 14` .... (3)

On comparing (1) and (3) we get

`h=-2,k=-1`

The center of first circle is (-2,-1).

Distance formula:

`D=√((x_2-x_1)^2+(y_2-y_1)^2)`

The distance between the centers of the circles

`D=√(\left(-2-1\right)^2+\left(-1-\left(-2\right)\right)^2)=√(10)`

Therefore, the distance between the centers of the circles is
`√(10)`.

Answer 2

The distance between both centers is 4.232

Explanation:

The formula of a circle with center in (h,k) and radius r is given by the formula

(x-h)² + (y-k)² = r²

The problem gives us the general formula of two circles so we're going to transform them into the center-radius formula to find the coordinates of the centers and then we'll find the distance between them.

The first circle is x²+y²-2x+4y-11=0

we are going to rearrange the terms of this equation and we get

(x² - 2x) + (y²+4y) = 11

we are going to complete it so the binomials become perfect trinomial squares:

(x²- 2x +1) + (y² + 4y + 4) = 11 + 1 + 4

(x-1)² + (y + 2)² = 16.

So this is a circle with center in (1, - 2) and radius 4.

We are going to do the same with the second circle:

x²+y²+4x+2y-9=0.

x² + 4x + y² + 2y = 9

(x²+ 4x + 4)² + (y² + 2y + 1)² = 9 +4 + 1

(x+2)² + (y + 1)² = 14

So this is a circle with center in (-2, 1) and radius √14

Now we need to find the distance between both centers which means finding the distance between the points (1, -2) and (-2, 1).

The formula for distance is given by:

`d= \sqrt{(x_(2)-x_(1) )^(2) +(y_(2) - y_(1))^2 }`

Substituting our points into the formula we get:

`d= \sqrt{(x_(2)-x_(1) )^(2) + (y_(2) - y_(1))^2 }\\d = √((-2-1)^2+ (1-(-2)^2) \\d=√((-3)^2+(3)^2)\\d=√(9+9) =√(18) = 4.242`

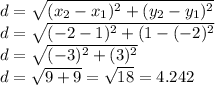
Therefore, the distance between the two centers is 4.242