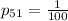Question

There are 100 equally spaced points around a circle. At 99 of the points, there aresheep, and at 1 point, there is a wolf. At each time step, the wolf randomly moves eitherclockwise or counterclockwise by 1 point. If there is a sheep at that point, he eats it.The sheep don’t move. What is the probability that the sheep who is initially oppositethe wolf is the last one remaining?

Answer 1

we have
`p_(51) = (1)/(100)`

Explanation:

considering circle with 100 points on it and then placing the wolf on one and sheep on rest.

pi = P( sheep on i-th spot is eaten at last}

As in the question we need to find probability of sheep opposite to the wolf, so p_{51}. observe each last spot is replaced by i-1 after eating

Byy LOTP we know thta
`pi = (1)/(2)pi-1 + (1)/(2)pi + 1, i \epsilon {2,... 99}`

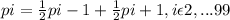
also these pi need to satisfy

`\sum_(i=1)^(100) pi =1`

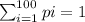
some sheep is eaten at last. Distribution is

`pi = (1)/(100)`

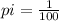
satisfies above equation, therefore we have
`p_(51) = (1)/(100)`