Question

Use the discriminant to predict the nature of the solutions to the equation 4x-3x²=10. Then, solve the equation.

Answer 1

Two imaginary solutions:

x₁=
`(2)/(3) -(1)/(3) i√(26)`

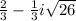
x₂ =
`(2)/(3) +(1)/(3) i√(26)`

Explanation:

When we are given a quadratic equation of the form ax² +bx + c = 0, the discriminant is given by the formula b² - 4ac.

The discriminant gives us information on how the solutions of the equations will be.

1. If the discriminant is zero, the equation will have only one solution and it will be real
2. If the discriminant is greater than zero, then the equation will have two solutions and they both will be real.
3. If the discriminant is less than zero, then the equation will have two imaginary solutions (in the complex numbers)

So now we will work with the equation given: 4x - 3x² = 10

First we will order the terms to make it look like a quadratic equation ax²+bx + c = 0

So:

4x - 3x² = 10

-3x² + 4x - 10 = 0 will be our equation

with this information we have that a = -3 b = 4 c = -10

And we will find the discriminant:
`b^(2) -4ac = 4^(2) -4(-3)(-10) = 16-120=-104`

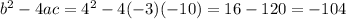
Therefore our discriminant is less than zero and we know that our equation will have two solutions in the complex numbers.

To proceed to solve the equation we will use the general formula

x₁= (-b+√b²-4ac)/2a

so x₁ =
`(-4+√(-104) )/(2(-3)) \\(-4+√(-104) )/(-6)\\(-4+2√(-26) )/(-6) \\(-4+2i√(26) )/(-6) \\(2)/(3) -(1)/(3) i√(26)`

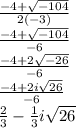
The second solution x₂ = (-b-√b²-4ac)/2a

so x₂=
`(-4-√(-104) )/(2(-3)) \\(-4-√(-104) )/(-6)\\(-4-2√(-26) )/(-6) \\(-4-2i√(26) )/(-6) \\(2)/(3) +(1)/(3) i√(26)`

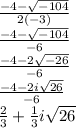
These are our two solutions in the imaginary numbers.