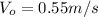Answer: 0.55 m/s
Step-by-step explanation:
This situation is related to projectile motion (also called parabolic motion), where the main equations are as follows:
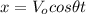 (1)
(1)
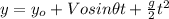 (2)
(2)
Where:
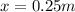 is the horizontal displacement of the pencil
is the horizontal displacement of the pencil
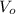 is the pencil's initial velocity
is the pencil's initial velocity
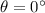 since we are told the pencil rolls horizontally before falling
since we are told the pencil rolls horizontally before falling
 is the time since the pencil falls until it hits the ground
is the time since the pencil falls until it hits the ground
 is the initial height of the pencil
is the initial height of the pencil
 is the final height of the pencil (when it finally hits the ground)
is the final height of the pencil (when it finally hits the ground)
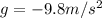 is the acceleration due gravity, always acting vertically downwards
is the acceleration due gravity, always acting vertically downwards
Begining with (1):
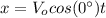 (3)
(3)
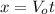 (4)
(4)
Finding
 from (2):
from (2):
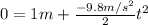 (5)
(5)
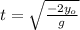 (6)
(6)
Substituting (6) in (4):
 (7)
(7)
Isolating
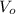 :
:
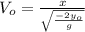 (8)
(8)
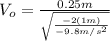 (9)
(9)
Finally: