Question

82. Use properties of exponents to rewrite each expression with only positive, rational exponents. Then find the numerical value of each expression when x = 9, y= 8, and z= 16. In each case, the expression evaluates to a rational number.

b. 11√y2z4

Answer 1

11yz² and when evaluating we get 22528

Explanation:

We have the expression
`11\sqrt{y^(2)z^(4)  }`

We know that a square root is a 1/2 exponent, so we're going to multiply the exponents of y and z by 1/2.

`11\sqrt{y^(2)z^(4)  }= 11y^(2(1/2))z^(4(1/2)) }  =11yz^(2)`

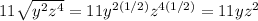
Therefore the expression is rewritten as
`11yz^2`

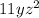
Now we're going to evaluate this expression for y = 8 and z = 16

`11yz^(2) =11(8)(16)^2=88(256)=22528`

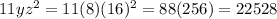
Thus, when evaluated the result is 22528