Question

A = ???? 4 −2

−1 3
????
1. Find the inverse of A. Show your work, and confirm your answer.
2. Explain why the matrix ????6 3
4 2
???? has no inverse

Answer 1

1.
`A^-^1=\left[\begin{array}{cc}(3)/(10)&(1)/(5)\\(1)/(10)&(2)/(5) \end{array}\right]`

2.
`|B|=0`

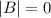
Explanation:

We have the matrix:

`A=\left[\begin{array}{cc}4&-2\\-1&3\end{array}\right]`

It's a 2×2 matrix (This means that the matrix has two rows and two columns).

1. We have to find the inverse of A.

For a 2×2 matrix the inverse is:

If you have
`A=\left[\begin{array}{cc}a&b\\c&d\end{array}\right]`

`A^-^1=(1)/(|A|) \left[\begin{array}{cc}d&-b\\-c&a\end{array}\right]`

And,

`|A|` is the determinant of the matrix, the determinant has to be different from zero.

If
`|A|=0` then the matrix doesn't have inverse.

`|A|=ad-bc`

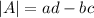
Then,

`A=\left[\begin{array}{cc}4&-2\\-1&3\end{array}\right]`

`a=4, b=-2, c=-1, d=3`

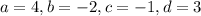
First we are going to calculate the determinant:

`|A|=ad-bc\\|A|=4.3-(-2).(-1)=12-2\\|A|=10`

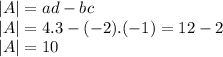
The determinant is different from zero, then the matrix has inverse.

Then the inverse of A is:

`A^-^1=(1)/(|A|) \left[\begin{array}{cc}d&-b\\-c&a\end{array}\right]`

`A^-^1=(1)/(10) \left[\begin{array}{cc}3&-(-2)\\-(-1)&4\end{array}\right]\\\\\\A^-^1=(1)/(10) \left[\begin{array}{cc}3&2\\1&4\end{array}\right]\\\\\\A^-^1=\left[\begin{array}{cc}(3)/(10)&(2)/(10)\\(1)/(10)&(4)/(10) \end{array}\right]\\\\\\A^-^1=\left[\begin{array}{cc}(3)/(10)&(1)/(5)\\(1)/(10)&(2)/(5) \end{array}\right]`

2. We have the matrix,

`B=\left[\begin{array}{cc}6&3\\4&2\end{array}\right]`

`a=6, b=3, c=4,d=2`

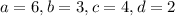
We have to calculate the determinant:

`|B|=ad-bc\\|B|=6.2-3.4=12-12\\|B|=0`

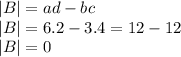
We said that a matrix can have an inverse only if its determinant is nonzero.

In this case
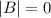`|B|=0` then, the matrix B doesn't have inverse.