Question

75. At age 25, you begin planning for retirement at 65. Knowing that you have 40 years to save up for retirement and expecting an interest rate of 4% per year compounded monthly throughout the 40 years, how much do you need to deposit every month to save up $2 million for retirement?

Answer 1

You need to deposit every month $1,692.10 every month, for 480 months, at a rate of 4% compounded monthly to obtain $2,000,000 in 40 years.

Explanation:

Hi, first, we need to convert that 4% compounded monthly rate into an effective monthly rate, that is by dividing by 12, which is 0.04/12=0.00333 or 0.333% effective monthly. Since the time periods are in years, they also need to be converted in months, this time we have to multiply 40 years by 12 and we get 480.

Finally ,we need to solve for "A" the following equation.

`Future Value=(A((1+r)^(n) -1)/(r)`

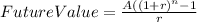
Where:

Future Value= 2,000,000

r = our effective monthly rate (0.00333)

n = periods to save (480 months)

So, it should look like this.

`2,000,000=(A((1+0.0033)^(480) -1))/(0.0033)`

`2,000,000=(A(3.939871133))/(0.00333)`

`2,000,000=A(1181.96134)`

`A=(2,000,000)/(1181.96134)`

`A=1,692.10`

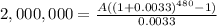
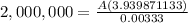
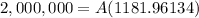
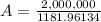
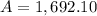
You will need to deposit $1,692.10 every month, for 480 months at a rate of 4% compounded monthly (0.333% effective monthly) in order to obtain $2,000,000 in 40 years.

Best of luck.

Answer 2

$1,709.00

Explanation:

First, let's convert the annualy interest rest (ia) to monthly(im):

(1 + im)¹² = 1 + ia

(1 + im)¹² = 1 + 0.04

(1 + im) =
`1.04^(1/12)`

im = 1.0033 - 1

im = 0.0033 = 0.33%

For an investiment, the final amount (A) can be calculated by:

`A = R*(((1+i)^n-1)/(i) )`

Where R is the amount invested per month, i is the interest, and n the number of months

n = 40*12 = 480 months

2,000,000 = R*((1+0.0033)⁴⁸⁰ - 1)/0.0033)

2,000,000 = R*1,170.22

R = $1,709.00