Question

71. Suppose that you currently have one credit card with a balance of $10,000 at an annual rate of 24.00% interest. You have stopped adding any additional charges to this card and are determined to pay off the balance. You have worked out the formulabn = b0r n − R(1 + r+r2 +....+ r n−1), where b0 is the initial balance, bn is the balance after you have maden payments, r= 1 + i, wherei is the monthly interest rate, and R is the amount you are planning to pay each month.

c. How long does it take to pay off this debt if you can afford to pay a constant $250 per month? Give the
answer in years and months.

Answer 1

It will take 71,35 months, wich can be rounded to 72, or 6 years

Explanation:

The debt will be paid when
`b_(n) = 0`, the formula can be written as:

`b_(n) = b_(0) r^(n) - R ((1-r^(n) )/(1-r) ) = 0`

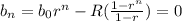
Solving for n:

`(R)/(1-r) = (b_(0)r^(n))/(1-r^(n) ) = (b_(0)r^(n))/(r^(n)((1)/(r^(n) ) -1) )`

`(1)/(r^(n)) = (b_(0)(1-r))/(R)+1= 0,28`

`r^(n)= (1)/(0,28) = 3,5714`

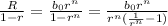
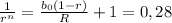
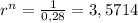
Solving the exponential equation:

`r^(n) = 3,5714 => n = log_(r) (3,5714) = (log(3,5714))/(log(r)) =71,35`

It will take 71,35 months, wich can be rounded to 72, or 6 years