Question

78. Use properties of exponents to rewrite each expression as either an integer or as a quotient of integers p/q to show the expression is a rational number.

a.4 √2. 4 √8

Answer 1

4√2 × 4√8 = 64, an integer.

Explanation:

a) 4√2 × 4√8

First let's remember that a square root can be rewritten as a 1/2 exponent,

Therefore the expression we have can be rewritten as

`4(2^(1/2) )4(8^(1/2))`

We are going to write all numbers in their prime factor expressions:

*Note: Remember that when we multiply two numbers with the same base but different exponents we sum up the exponents*

*Also, when we elevate one exponent to another exponent, we multiply the exponents*

`4(2^(1/2) )4(8^(1/2))\\=2^2 (2^(1/2))2^2 (2^(3))^(1/2) \\ =2^2 (2^(1/2))2^2 (2^(3/2))\\=2^22^2(2^(1/2)2^(3/2))\\=16(2^(4/2))\\=16(2^2)\\=16(4)\\=64`

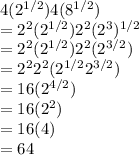
Therefore, the expression 4√2 × 4√8 = 64 and therefore is an integer