Question

Factor the following expression, and verify that the factored expression is equivalent to the original: 16x²-8x-3

Answer 1

Solved (x-3/4)(x+1/4)

Explanation:

16x²-8x-3=0

we can find the factors of the above quadratic equation using shridharacharya formula which given as

`x=(-b\pm √(b^2-4ac) )/(2a)`

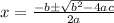
a= 16, b= -8 and c= -3 putting these values in above equation we can find the factors of x as

`x=(8\pm √(8^2-4*16*(-3)) )/(2*16)`

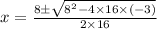
x= 3/4 and -1/4

now 16x²-8x-3 can also be written as (x-3/4)(x+1/4) as 3/4 and 1/4 are the roots of the equation.

on solving expression is equivalent to the original: 16x²-8x-3 we will again obtain 16x²-8x-3. Hence it is varified that the factored expression is equivalent to the original: 16x²-8x-3