Answer:
Ans. It wil take 346 months for you to save $160,000.
Explanation:
Hi, well, first, we need to find the equivalent effective rate (effective monthly) of 1% compounded monthly, that is, dividing it by 12.
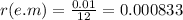
That is 0.0833% effective monthly, but we need to use the decimal representation in order to solve this problem. Now, we need to solve for "n" the following equation.
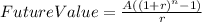
Where:
Future Value= 160,000
A=400
r= 0.000833
The answer is going to be in months, since the annuity (periodic saving) is monthly and the rate is effective monthly. Let´s solve this equation.
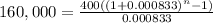
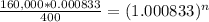
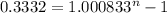
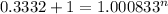
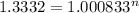
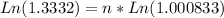
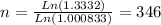
So, it will take 346 months (nearly 29 years) for your savings account to reach $160,000.
Best of luck.