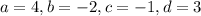Question

A = ???? 4 −2

−1 3
???? B = ????3 2
1 4
????
1. Is matrix A the inverse of matrix B? Show your work, and explain your answer.
2. What is the determinant of matrix B? Of matrix A?
Leson

Answer 1

1. The matrix A isn't the inverse of matrix B.

2. |B|=12, |A|=12

Explanation:

1. We want to know if matrix A is the inverse of matrix B, this means that if you do the product between B and A you have to obtain the identity matrix.

We have:

`A=\left[\begin{array}{cc}4&-2\\-1&3\end{array}\right]`

and

`B=\left[\begin{array}{cc}3&2\\1&4\end{array}\right]`

A and B are 2×2 matrices (2 rows and 2 columns), if you multiply them you have to obtain a 2×2 matrix.

Then if A is the inverse of B:

`B.A=I`

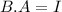
Where,

`I=\left[\begin{array}{cc}1&0\\0&1\end{array}\right]`

Observation:

If you have two matrices:

`A=\left[\begin{array}{cc}a&b\\c&d\end{array}\right]\\and\\B=\left[\begin{array}{cc}e&f\\g&h\end{array}\right]\\\\\\A.B=\left[\begin{array}{cc}(a.e+b.g)&(a.f+b.h)\\(c.e+d.g)&(c.f+d.h)\end{array}\right]`

Now:

`B.A=\left[\begin{array}{cc}3&2\\1&4\end{array}\right].\left[\begin{array}{cc}4&-2\\-1&3\end{array}\right]\\\\\\B.A=\left[\begin{array}{cc}4.3+(-2).1&4.2+(-2).4\\(-1).3+3.1&(-1).2+3.4\end{array}\right]\\\\\\B.A=\left[\begin{array}{cc}12-2&8-8\\-3+3&-2+12\end{array}\right]\\\\\\B.A=\left[\begin{array}{cc}10&0\\0&10\end{array}\right]`

`B.A=\left[\begin{array}{cc}10&0\\0&10\end{array}\right]\\eq \left[\begin{array}{cc}1&0\\0&1\end{array}\right]=I\\\\\\B.A\\eq I`

Then, the matrix A isn't the inverse of matrix B.

2. If you have a matrix A:

`A=\left[\begin{array}{cc}a&b\\c&d\end{array}\right]`

The determinant of the matrix is:

`|A|=ad-bc`

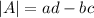
Then the determinant of B is:

`B=\left[\begin{array}{cc}3&2\\1&4\end{array}\right]`

`a=3, b=2, c=1, d=4`

`|B|=3.4-2.1\\|B|=12-2=10`

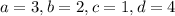
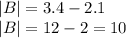
The determinant of A is:

`A=\left[\begin{array}{cc}4&-2\\-1&3\end{array}\right]`

`a=4, b=-2, c=-1, d=3`

`|A|=4.3-(-2).(-1)\\|B|=12-2=10`