Answer:
The solutions and the x-intercepts of the polynomial
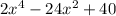 are:
are:
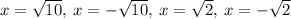
Explanation:
Given a function f a solution or a root of f is a value
 at which
at which
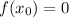 .
.
An x-intercept is a point on the graph where y is zero.
To find the solutions of the polynomial and the x-intercepts
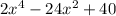 you need to:
you need to:
First, we need to factor the polynomial expression
Factor the common term
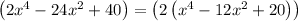
We can treat
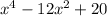 as a quadratic function with respect to
as a quadratic function with respect to

Let
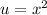 . We can rewrite
. We can rewrite
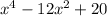 in terms of
in terms of
 as follows:
as follows:
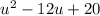
We need to solve the quadratic equation
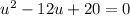
for this we can use the Quadratic Equation Formula:
For a quadratic equation of the form
 the solutions are
the solutions are
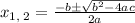
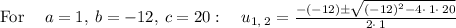

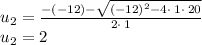
the solutions to the quadratic equation are:
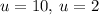
Therefore,
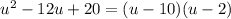
Recall that
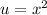 so
so
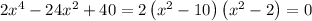
Using the Zero factor Theorem: If ab = 0, then either a = 0 or b = 0, or both a and b are 0.
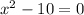 roots are
roots are
 ;
;
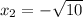
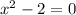 roots are
roots are
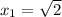 ;
;
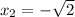
The solutions and the x-intercepts are:
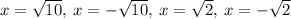
Because all roots are real roots the x-intercepts and the solutions are equal.