Question

49.The amount of caffeine in a patient’s bloodstream decreases by half every 3.5 hours. A latte contains 150 mg of caffeine, which is absorbed into the bloodstream almost immediately.

a. What type of function models the caffeine level in the patient’s bloodstream at time ???????? hours after drinking the latte? Explain how you know.

Answer 1

`C = \frac{C_(0) }{2^{(t)/(3.5) } }`

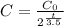
Explanation:

As the initial amount decreases by half every 3.5 hours, considering
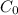`C_(0)` as the initial amount you have that:

at t=0 the amount would be
`C_(0)`

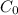
at t=3.5 the amount would be
`C_(0)/2`

at t=7 the amount would be
`C_(0)/4`

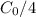
at t=10.5 the amount would be
`C_(0)/8`

and so on...

this behavior can the modeled as:

`C = \frac{C_(0) }{2^{(t)/(3.5) } }`

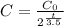
This matches all the points described above.