Answer:
1.
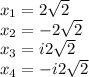
2.
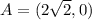 and
and
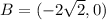
Explanation:
We have the expression
 to find the solutions we have to clear
to find the solutions we have to clear
 . Then,
. Then,
 Add 64 in both sides of the equation.
Add 64 in both sides of the equation.
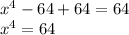
Now we have to re-write the equation:
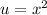 ⇒
⇒
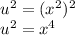
Then,

Apply square root on both members
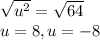
Now substitute back
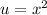
1.
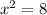
2.
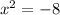
Solving for x:
1.
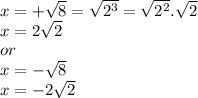
2.
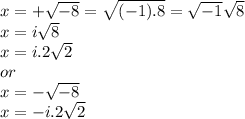
Then the solutions for
 are:
are:
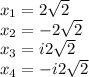
To find the x intercepts of the graph
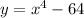 we have to replace with y=0.
we have to replace with y=0.
This means:

We already found the solutions for the expression, but we have to consider only the real solutions.
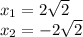
Because in a graph we can't have imaginary solutions.
Then the x intercepts of the graph are:
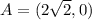 and
and
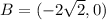
The graph of the function is: