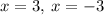Answer:
The solutions
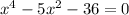 are
are
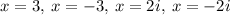 and the x-intercepts of
and the x-intercepts of
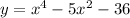 are
are
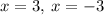
Explanation:
Finding the solutions to
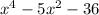 means finding the roots, a root is where the function is equal to zero.
means finding the roots, a root is where the function is equal to zero.
The x-intercept is the point at which the graph crosses the x-axis. At this point, the y-coordinate is zero.
To find the roots you need to:
Rewrite the equation with
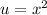 and
and
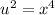

Solve by factoring
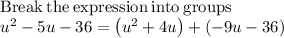
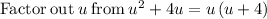




Using the Zero factor Theorem: if ab = 0 then a = 0 or b = 0 (or both a = 0 and b = 0)
The solutions to the quadratic equation are:
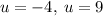
Substitute back
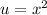 , solve for x
, solve for x
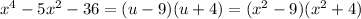
Apply the difference of squares formula

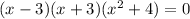
Using the Zero factor Theorem: if ab = 0 then a = 0 or b = 0 (or both a = 0 and b = 0)
The solutions are:
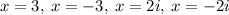
Because two of the solutions are complex roots the only x-intercepts are