Explanation:
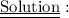
Let the present age of father be ' x ' years and that of the son be ' y ' years. From the first condition ,
- x = 2y ••••••• equation ( i )
From the second condition ,
- x - 12 = 3 ( y - 12 ) ••••• equation ( ii )
Substituting the value of x from equation ( i ) in equation ( ii ) :

Solve for y ( age of the son ) :
⟿
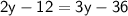
⟿
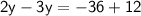
⟿
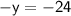
⟿
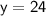
Now , Substituting the value of y in equation ( i ) , we get :
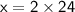
⟿
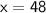
So, the present age of the father is 48 years and that of the son is 24 years.
Hope I helped ! ツ
Have a wonderful day / night ♡
▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁