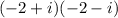Question

Write each of the following quadratic expressions as a product of linear factors. Verify that the factored form is equivalent.a)x²+12x+27b)x²-16c)x²+16d)x²+4x+5

Answer 1

(a) (x+3) (x+9)

(b) (x+4) (x-4)

(c) (x-4i) (x+4i)

(d) (-2+i) (-2-i)

Explanation:

We have given the quadratic expressions and we have to write these expressions in factor form

(a)
`x^2+12x+27`

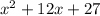
It can be written as
`x^2+9x+3x+27`

`x(x+9)+3(x+9)`

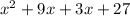
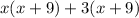
Now taking (x+9) as common

`(x+9)(x+3)`

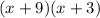
(b)
`x^2-16`

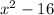
We know the algebraic equation
`a^2-b^2=(a+b)(a-b)`

`x^2-16=x^2-4^2=(x+4)(x-4)`

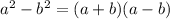
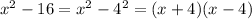
(c)
`x^2+16=(x-4i)(x+4i)`

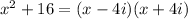
(d)
`x^2+4x+5`

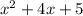
It can be written as
`(-2+i)(-2-i)`