Answer:
The equation has two x-intercepts. They are
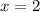 and
and
 .
.
Explanation:
A x-intercept are the values of x when
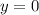 .
.
The number of x-intercepts is the number of solutions. The x-intercepts are the solutions.
So let's solve the equation:
We have the following equation:
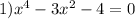 .
.
The first step to solve this problem is using
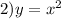
We replace in the equation 1, find the values of y, and then we replace in equation 2) to find the values of x.
To solve the equations, it is important to know how we find the roots of a second order polynomial.
Given a second order polynomial expressed by the following equation:
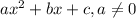
This polynomial has roots
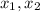 such that
such that
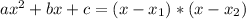 , given by the following formulas:
, given by the following formulas:
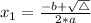
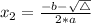
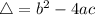
In this problem, we have

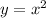
So
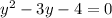
So:

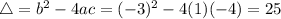
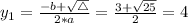
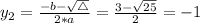
The values of y are

We also have that:
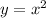
So
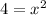
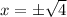

And

There is no real solution for this. So our only solutions are
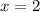 and
and
 .
.
So, the equation has two x-intercepts. They are
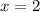 and
and
 .
.