c. -98 m/s
The motion of the rock is a uniformly accelerated motion (free fall) with constant acceleration
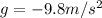 (negative since it is downward). Therefore, we can find its velocity using the following suvat equation
(negative since it is downward). Therefore, we can find its velocity using the following suvat equation
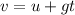
where
v is the final velocity
u is the initial velocity
g is the acceleration of gravity
t is the time
For the rock in the problem,
u = 0
So, its velocity at t = 10 s is
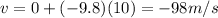
where the negative sign indicates that the velocity points downward.
d. -490 m
Since the motion is at constant acceleration, we can use another suvat equation:

where
s is the displacement
u is the initial velocity
g is the acceleration of gravity
t is the time
Substituting:
u = 0
t = 10 s
We find the rock's displacement:
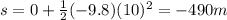
where the negative sign means the displacement is downward.