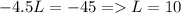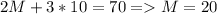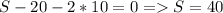Answer:
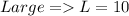
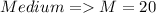
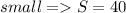
Explanation:
The number of small lemonades purchased is the number of mediums sold plus double the number of larges sold:
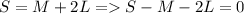
The total number of all sizes sold is 70:
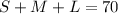
One-and-a-half times the number of smalls purchased plus twice the number of mediums sold is 100:
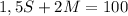
The system of equations is:

Matrix to solve by gauss-jordan elimination:
![\left[\begin{array}{cccc}1&-1&-2&0\\1&1&1&70\\1.5&2&0&100\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/high-school/i3cs1dbrtts6pc08ccymwdky1vs9pypvy6.png)
Solving from first row:
![\left[\begin{array}{cccc}1&-1&-2&0\\0&2&3&70\\0&3.5&3&100\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/high-school/d9g5gghk4ezoxt33z971gstagft083ehfc.png)
Solving from second row:
![\left[\begin{array}{cccc}1&-1&-2&0\\0&2&3&70\\0&0&-4.5&-45\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/high-school/tdkixvhelggajqsmzucbzvseam9lnqs4su.png)
From this: