Question

Find a formula for the product P of the solutions of the quadratic equation ax²+bx+c=0 .

Answer 1

product of the roots= c/a

Explanation:

The the two roots(α and β) of the quadratic equation ax²+bx+c=0 as given by shridharacharya formula are

`\alpha= (-b+√(b^2-4ac) )/(2a)`

`\beta= (-b-√(b^2-4ac) )/(2a)`

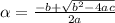
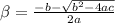
now product of the roots

αβ=
`(-b+√(b^2-4ac) )/(2a)`×
`(-b-√(b^2-4ac) )/(2a)`

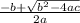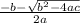
use formula (a+b)(a-b)= a^2-b^2 and solve we get

αβ= c/a

therefore product of the roots= c/a