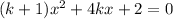Question

For what value of k are there two distinct real solutions to the original quadratic equation (k+1)x²+4kx+2=0.

Answer 1

k ∈ (-∞,
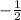`-(1)/(2)`)∪(1,∞)

Explanation:

For quadratic equations
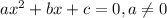`ax^2+bx+c=0,a\\eq 0` you can find the solutions with the Bhaskara's Formula:

`x_1=(-b+√(b^2-4ac))/(2a)\\and\\x_2=(-b-√(b^2-4ac))/(2a)`

A quadratic equation usually has two solutions.

If you only want real solutions the condition is that the discriminant (
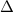`\Delta`) has to be greater than zero, this means:

`\Delta=b^2-4ac>0`

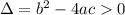
Then we have the expression:

`(k+1)x^2+4kx+2=0`

`a=(k+1)\\b=4k\\c=2\\`

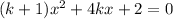
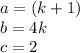
Now to find two distinct real solutions to the original quadratic equation we have to calculate the discriminant:

`b^2-4ac>0\\(4k)^2-4.(k+1).2>0\\16k^2-8(k+1)>0\\16k^2-8k-8>0`

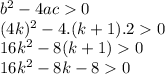
We got another quadratic function.

`16k^2-8k-8>0` we can simplify the expression dividing both sides in 8.

`16k^2-8k-8>0\\\\(16k^2)/(8) -(8k)/(8) -(8)/(8) >(0)/(8)\\\\2k^2-k-1>0`

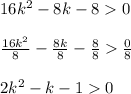
We can apply Bhaskara's Formula except that the condition in this case is that the solutions have to be greater than zero.

`2k^2-k-1>0\\a=2\\b=-1\\c=-1`

`k_1=(-(-1)+√((-1)^2-4.2.(-1)))/(2.2)=(1+√(9) )/(4)=(1+3)/(4) =1 \\and\\k_2=(-(-1)-√((-1)^2-4.2.(-1)))/(2.2)=(1-3)/(4)=-(2)/(4)=-(1)/(2)`

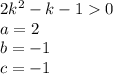
Then,

`k>1 \\and\\k<-(1)/(2)`

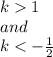
The answer is:

For all the real values of k who belongs to the interval:

(-∞,
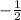`-(1)/(2)`)∪(1,∞)

there are two distinct real solutions to the original quadratic equation
`(k+1)x^2+4kx+2=0`