Answer:
C
Explanation:
We can use the vertex form of a quadratic equation, given by:

Where a is the leading coefficient and (h, k) is the vertex.
We are given that the vertex is (-3, 1).
Hence, h = -3 and k = 1. By substitution:

Simplify:
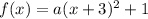
With this, we can eliminate B and D.
Notice that our parabola is curving downwards.
Therefore, our leading coefficient must be negative.
The only choice that leaves us with is C.
So, our function is:

And our final answer is C.