Answer:
If
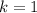 or
or
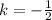 , there is only one solution to the given quadratic equation.
, there is only one solution to the given quadratic equation.
Explanation:
Given a second order polynomial expressed by the following equation:
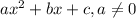
This polynomial has roots
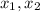 such that
such that
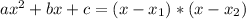 , given by the following formulas:
, given by the following formulas:
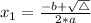
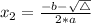
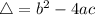
The signal of
 determines how many real roots an equation has:
determines how many real roots an equation has:
 : Two real and different solutions
: Two real and different solutions
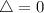 : One real solution
: One real solution
 : No real solutions
: No real solutions
In this problem, we have the following second order polynomial:
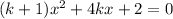 .
.
This means that
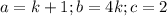
It has one solution if
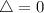
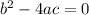
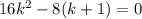
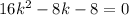
We can simplify by 8
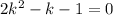
The solution is:
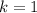 or
or
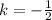
So, if
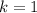 or
or
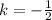 , there is only one solution to the given quadratic equation.
, there is only one solution to the given quadratic equation.