Question

Suppose we have a quadratic equation ax²+bx+c=0 so that a+c=0.Does the quadratic equation have one solution or two distinct solutions? Are they real or complex? Explain how you know.

Answer 1

The roots of equation are real and distinct.

Explanation:

Given that

ax²+bx+c=0

a+c=0

To find the behavior of roots we have to find out D

`D=√(b^2-4ac)`

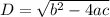
If

D> 0 Two real distinct roots

D=0 Two equal roots

D<0 Tow imaginary roots

`D=√(b^2-4ac)`

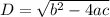
a+c=0

a= - c

`D=√(b^2-4* (-c)* c)`

`D=√(b^2+4* c^2)`

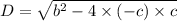
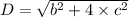
It means that D>0 .So the roots of equation is real and distinct.