Question

Find all real and complex solutionsa)x²+2x+1=0b)x²+4=0c)9x²-4x-14=0d)8x²+4x+32=0

Answer 1

Explanation:

a). x²+2x+1=0

`\left ( x + 1 \right )^(2)=0`

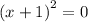
x = -1 , - 1

Therefore the roots are real.

b). x²+4=0

x²= -4

x = 2 , -2

Therefore the roots are real.

c) 9x²-4x-14 =0

x =
`\frac{-4\pm \sqrt{-4^(2)-(4* 9* -14)}}{2* 9}`

=
`(-4\pm √(16+504))/(18)`

=
`(-4\pm √(520))/(18)`

=
`(-4\pm 22.8)/(18)`

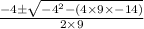
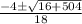
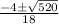
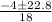
x =
`(-4- 22.8)/(18)`

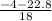
= -1.48

x =
`(-4+ 22.8)/(18)`

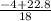
= 1.04

Therefore, x = 1.04 , -1.48

Hence the roots are real

d) 8x²+4x+32=0

x =
`\frac{-4\pm \sqrt{4^(2)-(4* 8* 32)}}{2* 8}`

=
`(-4\pm √(16-1024))/(16)`

=
`(-4\pm √(1008))/(16)`

=
`(-4\pm 31.7)/(16)`

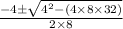
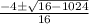
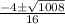
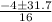
x =
`(-4- 31.7)/(16)`

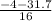
= -2.2

x =
`(-4+ 31.7)/(16)`

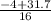
= 1.73

Therefore, x = 1.73 , -2.2

Hence the roots are real