Question

Show that if k>3.2, the solutions of 5x²-8x+k=0 are not real numbers.

Answer 1

3.2 is the highest value for k that will yield a non-negative discriminant

Explanation:

For an equation to have real numbers as solutions, its discriminant (delta value) must be bigger than zero since there are no real square root solutions for negative numbers.

`x_(1) =(-b +√(\Delta) )/(2a)\\x_(2) =(-b -√(\Delta) )/(2a)`

In this case, the discriminant is given by:

`\Delta = (-8)^(2) - 4*5*k \\\Delta = 64 - 20*k \\`

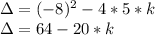
For k =3.2

`\Delta = 64 - 64 = 0 \\`

As shown above, 3.2 is the highest value for k that will yield a non-negative discriminant and, therefore, if k > 3.2 the solutions of the expression are not real numbers.