Answer:
a)
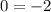 is not a valid equality. So a) will not have a solution set of all real numbers.
is not a valid equality. So a) will not have a solution set of all real numbers.
b)
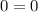 is a valid equality for all real numbers. So b) will have a solution set of all real numbers.
is a valid equality for all real numbers. So b) will have a solution set of all real numbers.
c)
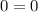 is a valid equality for all real numbers. So c) will have a solution set of all real numbers.
is a valid equality for all real numbers. So c) will have a solution set of all real numbers.
d)
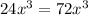 is only valid for
is only valid for
 . So d) will not have a solution set of all real numbers.
. So d) will not have a solution set of all real numbers.
Explanation:
a)


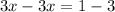
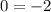
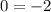 is not a valid equality. So a) will not have a solution set of all real numbers.
is not a valid equality. So a) will not have a solution set of all real numbers.
b)

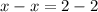
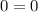
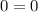 is a valid equality for all real numbers. So b) will have a solution set of all real numbers.
is a valid equality for all real numbers. So b) will have a solution set of all real numbers.
c)
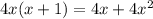
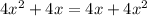
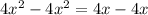
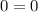
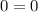 is a valid equality for all real numbers. So c) will have a solution set of all real numbers.
is a valid equality for all real numbers. So c) will have a solution set of all real numbers.
d)
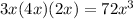
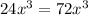
This is only valid for
 . So d) will not have a solution set of all real numbers.
. So d) will not have a solution set of all real numbers.