Question

Find the multiplicative inverse of 3 − 2i. Verify that your solution is corect by confirming that the product of

3 − 2i and its multiplicative inverse is 1.
2. What

Answer 1

`(3)/(13) + (2i)/(13)`

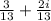
Explanation:

The multiplicative inverse of a complex number y is the complex number z such that (y)(z) = 1

So for this problem we need to find a number z such that

(3 - 2i) ( z ) = 1

If we take z =
`(1)/(3-2i)`

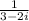
We have that

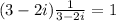`(3- 2i)(1)/(3-2i) = 1` would be the multiplicative inverse of 3 - 2i

But remember that 2i = √-2 so we can rationalize the denominator of this complex number

`(1)/(3-2i ) ((3+2i)/(3+2i ) )=(3+2i)/(9-(4i^(2) )) =(3+2i)/(9-4(-1)) =(3+2i)/(13)`

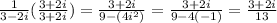
Thus, the multiplicative inverse would be
`(3)/(13) + (2i)/(13)`

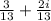
The problem asks us to verify this by multiplying both numbers to see that the answer is 1:

Let's multiplicate this number by 3 - 2i to confirm:

`(3-2i)((3+2i)/(13)) = (9-4i^(2) )/(13)  =(9-4(-1))/(13)= (9+4)/(13) = (13)/(13)= 1`

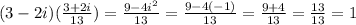
Thus, the number we found is indeed the multiplicative inverse of 3 - 2i