Answer:
x = y²
Explanation:
Given:
log(x) = log(y) + log(z) + log(y) − log(z) ................(1)
Now,
from the properties of natural log, we have
log(A) + log(B) = log(AB)
and
log(A) - log(B) =
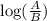
applying the above property in the provided equation, we have
log(x) = ( log(y) + log(z) ) + log(y) − log(z)
or
log(x) = log(yz) + log(y) - log(z)
or
log(x) = log(yzy) - log(z) [as log(yz) + log(y) = log(yzy) ]
or
log(x) = log(y²z) - log(z)
also,
log(x) =
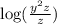
or
log(x) = log(y²)
Now, taking the anti-log both sides, we get
x = y²