Question

Solve the following equations.
log2(x^2 − 16) − log^2(x − 4) = 1

Answer 1

`x=(4*(2+e))/(e-2)`

Explanation:

Let's rewrite the left side keeping in mind the next propierties:

`log((1)/(x) )=-log(x)`

`log(x*y)=log(x)+log(y)`

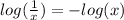
Therefore:

`log(2*(x^(2) -16))+log((1)/((x-4)^(2) ))=1\\ log((2*(x^(2) -16))/((x-4)^(2)))=1`

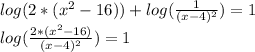
Now, cancel logarithms by taking exp of both sides:

`e^{log((2*(x^(2) -16))/((x-4)^(2)))} =e^(1) \\(2*(x^(2) -16))/((x-4)^(2))=e`

Multiply both sides by
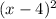`(x-4)^(2)` and using distributive propierty:

`2x^(2) -32=16e-8ex+ex^(2)`

Substract
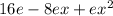`16e-8ex+ex^(2)` from both sides and factoring:

`-(x-4)*(-8-4e-2x+ex)=0`

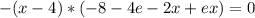
Multiply both sides by -1:

`(x-4)*(-8-4e-2x+ex)=0`

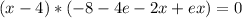
Split into two equations:

`x-4=0\hspace{3}or\hspace{3}-8-4e-2x+ex=0`

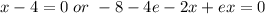
Solving for
`x-4=0`

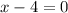
Add 4 to both sides:

`x=4`

Solving for
`-8-4e-2x+ex=0`

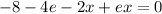
Collect in terms of x and add
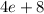`4e+8` to both sides:

`x(e-2)=4e+8`

Divide both sides by e-2:

`x=(4*(2+e))/(e-2)`

The solutions are:

`x=4\hspace{3}or\hspace{3}x=(4*(2+e))/(e-2)`

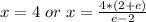
If we evaluate x=4 in the original equation:

`log(0)-log(0)=1`

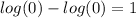
This is an absurd because log (x) is undefined for
`x\leq 0`

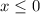
If we evaluate
`x=(4*(2+e))/(e-2)` in the original equation:

`log(2*(((4e+8)/(e-2))^2-16))-log(((4e+8)/(e-2)-4)^2)=1`

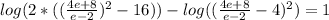
Which is correct, therefore the solution is:

`x=(4*(2+e))/(e-2)`