Question

Describe the sequence of transformations that would take the graph of f(x)=x² to each parabola described below. Focus: (1/4,0),directrix: x=-1/4

Answer 1

The parabola obtained is x=y²

Explanation:

Given the focus (1/4,0) and directrix: x=-1/4

A point on the parabola is determined by the distance of that point with the focus and with the directrix:

Distance between the parabola and the directrix:
`\sqrt{(x+(1)/(4))^(2)  }`

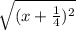
Distance between the parabola and the focus:
`\sqrt{(x-(1)/(4))^(2) +(y-0)^(2) }`

`\sqrt{(x+(1)/(4))^(2)}`=
`\sqrt{(x-(1)/(4))^(2) +(y-0)^(2) }`

`(x+(1)/(4))^(2)`=
`(x-(1)/(4))^(2) +(y-0)^(2)`

`x^2+(1)/(2) x+(1)/(16) = x^2-(1)/(2) x+(1)/(16) + y^(2)`

`(1)/(2) x=-(1)/(2) x + y^(2)`

`(1)/(2) x+(1)/(2) x = y^(2)`

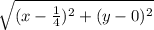
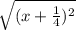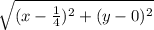
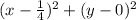
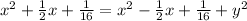
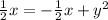
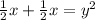
x=y²