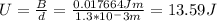Answer:
a) The stored energy is 4.34 J
b) The stored energy is 13.59 J
Step-by-step explanation:
A capacitor stores energy in its electric field according to the following formula:
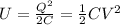
Where U is the stored energy, Q the charge on a plate, V the voltage between plates and C its capacity.
When we change the distance between the plates,capacity changes, as:
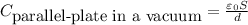
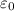 and S (area of the plate) remain constant, but d (distance between changes) makes capacity vary.
and S (area of the plate) remain constant, but d (distance between changes) makes capacity vary.
a) Charge remains constant (as it is disconnected from the circuit) but capacity changes.
As only d changes, we express C as a function of d and we find the new internal energy:
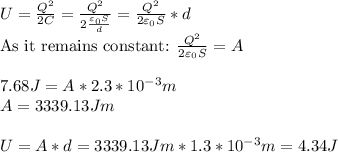
b) Voltage remains constant, but capacity changes:
Knowing that, expressing C as a function of d:
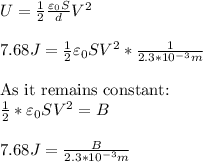
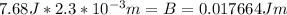
Knowing the value of the constant, we calculate the new internal energy: