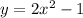Question

Write the equation of a parabola similar to y=2x² that does NOT contain the point (0,0) but does contain the point (1,1).

Answer 1

`y=2x^(2) -1`

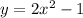
Explanation:

For a parabolic equation to NOT contain the point (0,0) it must have a numeric constant independent from both x and y variables, so the general form would be as follows:

`y=2x^(2) +c`

Solving the equation for the point (1,1) would give the necessary value for the constant "c" to make the equation valid:

`y=2x^(2) +c\\1=2*(1)^(2) +c\\c = 1 -2 = -1`

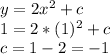
Therefore, the equation that meets both of the required conditions is:

`y=2x^(2) -1`