Question

2 ln(x + 2) − ln(−x) = 0

Answer 1

`x=-1`

Explanation:

Rewrite the equation using the next propierties:

`log((1)/(x) )=-log(x)`

`ylog(x)=log(x^(y) )`

`log(x*y)=log(x)+log(y)`

`ln((x+2)^2)+ln((-1)/(x) )=0\\ln(((x+2)^2)/(-x))=0`

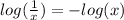
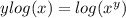
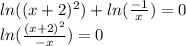
Cancel logarithms by taking exp of both sides:

`((x+2)^2)/(-x) =e^(0) =1`

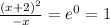
Multiplying both sides by -x and factoring:

`x^(2) +5x+4=0`

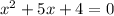
Factoring:

`(x+1)(x+4)=0`

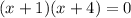
The solutions are:

`x=-1\hspace{3}or\hspace{3}x=-3`

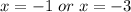
Evaluating x=-4

`2ln(-2)-(4)=0`

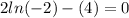
This is an absurd because ln(x) is undefined for
`x\leq 0`

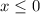
Evaluating x=-1

`2ln(1)-ln(1)=0\\0-0=0`

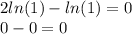
Which is correct, hence the solution is:

`x=-1`