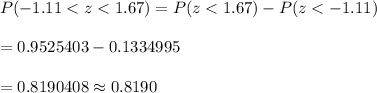Answer: a) 0.8665
b) 0.8190
Explanation:
Given : The partial pressure of oxygen PaO2 is a measure ofthe amount of oxygen in the blood. Assume that the distribution ofPaO2 levels among newborns has a
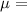 38 mmHg and
38 mmHg and
 9 mmHg.
9 mmHg.
If we take a random sample n= 25 newborns, then using formula
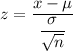 , we have
, we have
At x= 36
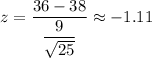
At x= 41

Using table for z-values, the probability that the sample mean will be greater than 36 :
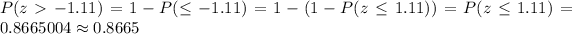
The probability that the sample mean will be between 36 and 41 :-