Answer:
x = 6.404
Explanation:
The given equation is:
63ˣ = 36⁽ˣ⁺¹⁾
Taking log on both side
x log(63) = (x + 1) log(36)
⇒ x log(63) = x log(36) + log(36)
⇒ x log(63) - x log(36) = log(36)
⇒ x {log(63) - log(36)} = log(36)
⇒

⇒
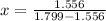 {∵ log(36) = 1.556 and log(63) = 1.779}
{∵ log(36) = 1.556 and log(63) = 1.779}
⇒ x = 6.404