Question

Let P be the parabola with focus (0,4) and directrix y=x.Write an equation whose graph is a parabola with a vertical directrix that is congruent to P.

Answer 1

y²=4√2.x

Explanation:

The focus is at (0,4) and directrix is y=x or x-y =0, for a parabola P.

The distance between the focus and the directrix of the parabola P is

`\frac {\sqrt{(1)^(2)+(-1)^(2)  } }`=
`(4)/(√(2) )`

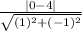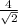
{Since the perpendicular distance of a point (x1, y1) from the straight line ax+by+c =0 is given by
`\frac {\sqrt{a^(2)+b^(2)  } }` }

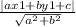Let us assume that the equation of the parabola which is congruent with parabola P is y²=4ax

{Since the parabola has vertical directrix}

Hence, the distance between focus and the directrix is 2a =
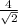`(4)/(√(2) )`, {Two parabolas are congruent when the distances between their focus and the directrix are same}

⇒ a=√2

Therefore, the equation of the parabola is y²=4√2.x (Answer)