Question

Ln(x + 2) = ln(12) − ln(x + 3)

Answer 1

x = 1 , -6

Explanation:

given,

ln (x + 2) = ln (12) − ln (x + 3)

using identity of logarithm

ln (ab) = ln (a) + ln (b)

ln (a) - ln(b) = ln (a/b)

now

ln (x + 2) = ln (12) − ln (x + 3)

ln (x + 2) =
`ln ((12)/(x+3))`

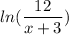
on comparing

`x + 2 = (12)/(x+3)`

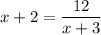
(x+2)(x+3) = 12

x² + 5 x + 6 = 12

x² + 5 x - 6 = 0

x² + 6 x - x - 6 = 0

x(x + 6) -1 (x+ 6) = 0

(x - 1)(x + 6) = 0

x = 1 , -6

Hence, the value of x comes out to be x = 1 , -6