Question

Sketch each parabola, labeling its focus and directrix. y=(1/10)(x-1)²-2

Answer 1

The equation of parabola is
`y=(1)/(10)\left(x-1\right)^(2)-2`

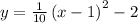
Comparing with the vertex form of the parabola:
`y=a(x-h)^2+k`

`a=(1)/(10),h=1,k=-2`

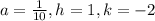
Hence, the vertex of the parabola is given by (h,k) = (1, -2)

Now, vertex is the midpoint of the focus and the point on the directrix.

Distance, between vertex and focus is p and that of point on the directrix is p.

Now, let us find p

`p=(1)/(4a)\\\\p=(1)/(4\cdot1/10)\\\\p=(5)/(2)`

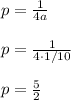
Thus, the focus is given by

`(h,k+p)\\\\=(1,-2+5/2)\\\\=(1,1/2)=(1,0.5)`

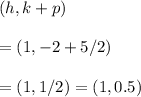
And the directrix is given by

`y=k-p\\\\y=-2-5/2\\\\y=-(9)/(2)`

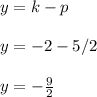
Since, a >0 hence, it is an upward parabola.

The graph is shown in the attached file.