Question

. Write each number in terms of natural logarithms, and then use the properties of logarithms to show that it is a

rational number.
log9(√27)

Answer 1

The answer is 3/4

Explanation:

Hi, we need to change the base of the logarithm, for that we need to use the following formula.

`Log_(b) (a)=(Ln(a))/(Ln(b))`

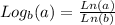
In our case, this is:

`Log_(9) (√(27) )=(Ln(√(27) ))/(Ln(9))`

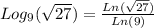
Which is the same as:

`\frac{Ln(27)^{(1)/(2) }}{Ln(9)}`

Now, let´s solve this using the log properties

`(1)/(2) ((Ln(27))/(Ln(9)) )`

`(1)/(2) ((Ln(9*3))/(Ln(9)) )`

`(1)/(2) ((Ln(9)+Ln(3))/(Ln(9)) )`

`(1)/(2) ((Ln(9))/(Ln(9))+(Ln(3))/(Ln(9))  )\\`

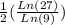
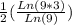
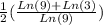
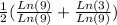
We can change 3 for 9^(1/2)

`(1)/(2) ((Ln(9))/(Ln(9))+\frac{Ln(9^{(1)/(2) } )}{Ln(9)}  )\\`

`(1)/(2) ((Ln(9))/(Ln(9))+(Ln(9 ))/(2*Ln(9))  )\\`

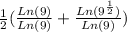
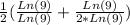
Since Ln(9) / Ln(9) =1, we get.

`(1)/(2) (1+(1)/(2) )`

`(1)/(2) ((3)/(2) )=(3)/(4)`

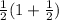
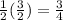
Best of luck.