Answer:
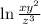
Explanation:
Data provided:
ln(x) + 2 ln(y) − 3 ln(z)
Now,
From the properties of log function,
ln(A) + ln(B) = ln(AB)
n × ln(x) = ln(xⁿ)
and,
ln(A) - ln(B) =
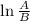
applying the properties in the given equation
we get
⇒ ln(x) + 2 ln(y) − 3 ln(z)
or
⇒ ln(x) + ln(y²) - ln(z³) (using n × ln(x) = ln(xⁿ))
or
⇒ ln(xy²) - ln(z³) (using ln(A) + ln(B) = ln(AB) )
or
⇒
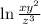 (using ln(A) - ln(B) =
(using ln(A) - ln(B) =
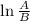 )
)