Answer:
The demonstration is showed below
Explanation:
The distance betwenn two points is given by:

If the point is equidistant from a point and a line, the distance must be equal. For the line let's select the point (x,-4), because the distance will be ortogonal, and is the small distance between a point and a line. So:
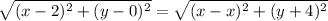
Removing the squares:
(x-2)² + y² = (y+4)²
(x-2)² + y² = y² + 8y + 16
y² - y² - 8y = 16 - (x-2)²
8y = (x-2)² - 16
y = (1/8)*(x-2)² - 16/8
y = (1/8)*(x-2)² - 2