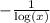Question

Rewrite each expression in an equivalent form that only contains one base 10 logarithm.

logx (1/10), for positive real values of x ≠ 1

Answer 1

`-(1)/(\log(x))`

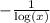
Explanation:

Data provided:

logₓ (1/10)

Now,

From the properties of log function

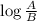`\log(A)/(B)` = log(A) - log(B)

logₓ (z)=
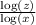`(\log(z))/(\log(x))` (where the base of the log is equal for both numerator and the denominator)

also,

log(xⁿ) = n × log(x)

Therefore,

logₓ (1/10) = logₓ(1) - logₓ(10)

=
`(\log(1))/(\log(x)) - (\log(10))/(\log(x))` (here log = log₁₀)

=
`(0)/(\log(x)) - (\log(10))/(\log(x))` (as log(1) = 0)

=
`-(\log(10))/(\log(x))`

=
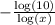
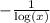`-(1)/(\log(x))` (as log(10) = 1)

Therefore,

the given equation can be rewritten as
`-(1)/(\log(x))`